ニュートン法(Newton’s method)は、数値計算を通じて非線形方程式の解を近似的に求める効率的な手法です。
この方法は、特定の条件下で解に非常に速く収束し、数回の計算で精度の高い解を得ることができます。
本記事では、ニュートン法の基本的な概念、計算の流れ、そしてその利点を詳しく解説します。
さらに、実際の問題にどのように適用できるかについても触れます。
ニュートン法の基本概念
ニュートン法とは?
ニュートン法は、方程式の解を数値的に求める方法の一つで、特に非線形方程式に対して非常に有効です。
この方法は、関数の接線を利用して解に収束するプロセスに基づいています。
具体的には、次のように進行します:
-
初期値を設定し、その点での接線を求める。
-
接線のx軸との交点を計算し、その値を新しい推定値として設定。
-
再度接線を求め、交点を計算することを繰り返し行う。
このプロセスを繰り返すことで、xの値が解に収束し、最終的に精度の高い近似値が得られます。
ニュートン法の計算の流れ
ニュートン法の数式
ニュートン法を数式で表すと次のようになります。
方程式 f(x) = 0 を解くために、初期値 x₀ から始め、次の式で新しい推定値 xₙ₊₁ を計算します。
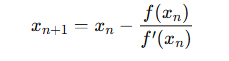
ここで、f(x) は求めたい解を含む関数、f'(x) はその微分です。
この式を繰り返し適用することで、解に収束するのです。
ニュートン法の適用条件
ニュートン法は次のような条件が満たされている場合に適用できます:
-
関数が微分可能であること(一次導関数が存在する)。
-
関数が単調増加または単調減少していること。
-
解を求める範囲内で、関数が下に凸であること(すなわち、最小値が存在する場合に最も効果的です)。
これらの条件が満たされると、ニュートン法は効率よく収束し、非常に高精度な解を短期間で得ることができます。
ニュートン法の利点と欠点
ニュートン法の利点
-
収束速度が速い: ニュートン法は、特に解に近い初期値が与えられた場合、非常に速く収束します。
-
例えば、二分法に比べてはるかに少ない計算回数で精度の高い解を得ることができます。
-
計算効率が良い: 初期値を適切に設定すれば、数回の反復で解が得られ、計算リソースを無駄にすることがありません。
ニュートン法の欠点
-
初期値に依存: 初期値が不適切な場合、解に収束しないことがあります。
-
特に解が複数ある場合や関数が凸でない場合には、収束しないことがあります。
-
導関数の計算が必要: 数値的に解を求める際、関数の導関数を計算する必要があるため、微分可能な関数に限られます。
実際の利用例:ニュートン法の応用
数値解析におけるニュートン法
ニュートン法は、物理学、工学、経済学など多くの分野で数値解析の一部として利用されています。
例えば、非線形方程式の解法において、ニュートン法は非常に効果的です。
例: 非線形方程式の解法
例えば、以下の非線形方程式 f(x) = x² – 2 = 0 を解くときに、ニュートン法を使用できます。
関数の微分は f'(x) = 2x です。初期値 x₀ = 1 から開始すると、ニュートン法を適用することで、x = √2 の解に収束します。
科学技術計算
ニュートン法は、特に数値シミュレーションや物理モデルの解析において重要です。
たとえば、流体力学や熱力学のシミュレーションにおいて、非線形方程式が頻繁に現れるため、解法としてニュートン法が採用されます。
まとめ
ニュートン法は、非線形方程式の解を効率よく近似するための強力な数値計算手法です。
解の収束速度が速く、計算効率が高いため、多くの実務的な問題において利用されています。
ただし、適切な初期値と導関数の計算が必要なため、特定の条件下での使用が推奨されます。
数学的な解法を数値的に求める際には、ニュートン法が非常に重要な役割を果たします。
この方法を理解し、さまざまな問題に応用することで、より複雑な問題に対しても迅速に解決策を見出すことが可能となります。
