仮数(significand)は、浮動小数点数の表現において、数値の有効数字を示す重要な要素です。
この概念は、コンピュータ科学や数値計算の分野で広く利用されており、データの精度と表現方法に直接影響を与えます。
本記事では、仮数の定義、浮動小数点数との関係、具体例、および実際の応用について詳しく説明します。
仮数の基本概念
仮数とは?
仮数は、浮動小数点数を表現する際に使用される数値の一部で、数の有効数字を示します。
具体的には、数値を「仮数 × 基数^指数」の形式で表現し、仮数がその数の有効桁を構成します。
この形式により、数値の大きさにかかわらず、常に同じ精度で数値を表現できます。
浮動小数点数の構造
浮動小数点数は次のような構造を持ちます:
- 仮数: 実際の数字の部分。
- 基数: 通常は10(十進数)または2(2進数)。
- 指数: 基数がどれだけの桁数を移動するかを示す。
たとえば、数値「573.765」を浮動小数点数として表現する場合、次のようになります:
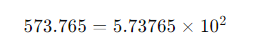
ここで、仮数は「5.73765」、指数は「2」となります。
仮数の位置
仮数の小数点の位置は自由に決められますが、表現形式に関する規約を定めておく必要があります。
例えば、仮数を整数として表すことも可能で、その場合の表現は次のようになります:
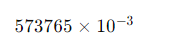
この場合、仮数は「573765」、指数は「-3」となります。
コンピュータにおける仮数の表現
コンピュータでは、すべての情報は「0」と「1」の組み合わせで表現されるため、仮数と指数も通常は2進数で表現されます。
多くの場合、基数にも2を使用します。
IEEE 754という浮動小数点数の標準規格では、基数2の形式と基数10の形式の両方が定義されています。
IEEE 754規格
IEEE 754規格は、浮動小数点数の表現方法に関する国際的な基準です。
この規格により、さまざまな数値データの処理が標準化され、異なるシステム間での互換性が確保されます。
仮数と指数の形式に関する具体的なルールもここに含まれています。

実際の応用例
科学技術計算
浮動小数点数と仮数は、科学技術計算において極めて重要です。
たとえば、物理シミュレーションやデータ分析では、非常に大きな数値や非常に小さな数値を扱う必要があります。
仮数を使用することで、数値の精度を保ちながら計算を行うことができます。
プログラミングにおける使用
プログラミング言語では、浮動小数点数を扱うためのデータ型が用意されています。
たとえば、PythonやJavaでは、float型やdouble型が使用され、これらは内部で仮数と指数を持つ浮動小数点数として実装されています。
プログラマーは、これらのデータ型を利用することで、計算の精度を保ちながら数値を操作できます。
まとめ
仮数は、浮動小数点数の表現において欠かせない要素であり、数値の有効数字を示す重要な役割を果たします。
コンピュータ科学において、仮数の理解は数値計算やデータ分析において不可欠です。
IEEE 754規格により、異なるシステム間での数値データの互換性が確保されており、仮数の概念を適切に活用することで、より精度の高い計算が可能となります。
さらに参考してください。
