**四分位数(quartile point)**は、統計学において数値データの集合を分析するための重要な指標です。
本記事では、四分位数の定義、計算方法、実用的な応用について詳しく解説します。
四分位数を理解することで、データの分布やばらつきをより正確に把握できるようになります。
四分位数の基本概念
四分位数の定義
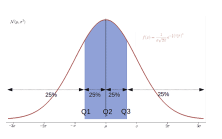
四分位数とは、データを昇順に並べたときに、同じ数ずつ4等分するための3つの区切りのことを指します。
具体的には、以下の3つの四分位数があります:
- 第1四分位数(Q1): 下から1/4の位置にある値
- 第2四分位数(Q2): 中央の値(中央値)
- 第3四分位数(Q3): 下から3/4の位置にある値
このように、四分位数はデータの分布を理解するための重要な指標です。
パーセンタイルとの関係
四分位数は、パーセンタイル(percentile)とも密接に関連しています。
具体的には:
- 第1四分位数は25パーセンタイル
- 第2四分位数は50パーセンタイル
- 第3四分位数は75パーセンタイル
これにより、データが全体の中でどの位置にいるかをより具体的に示すことができます。
四分位数の計算方法
データの整理
四分位数を計算するためには、まずデータを昇順に並べます。
次に、以下の手順で各四分位数を求めます:

例
例えば、データセットが{3, 1, 4, 2, 5}の場合:

この例では、Q1が1.5、Q2が3、Q3が4.5となります。
四分位範囲と四分位偏差
四分位範囲(IQR)
四分位範囲は、データのばらつきを示す指標で、以下のように定義されます:
四分位範囲(IQR)=Q3−Q1
この値が小さいほど、データが中心付近に集中していることを示します。
四分位偏差
四分位範囲の半分を四分位偏差(quartile deviation)と呼びます。
これは、データの散らばり具合を示す指標として広く使用されています。
まとめ
四分位数は、データの分布を理解するための重要な指標であり、データ分析や統計学において欠かせない概念です。
第1四分位数、第2四分位数、第3四分位数を理解することで、データの特性をより深く把握できるようになります。四分位範囲や四分位偏差を活用することで、データのばらつきや集中度を評価し、より正確な分析を行いましょう。
さらに参考してください。
