回帰分析(regression analysis)は、データ解析や統計学で広く利用されている強力な手法です。
原因と結果の関係を明らかにし、予測やシミュレーションを行うための基本的な技術です。
本記事では、回帰分析の基本概念から、単回帰分析と重回帰分析、さらに非線形回帰の違いまでを詳しく解説し、実際のビジネスや研究における応用例を紹介します。
回帰分析とは?
基本概念
回帰分析は、ある結果(従属変数)が他の数値(説明変数)によってどのように影響を受けるかを明らかにするための手法です。
これにより、因果関係の推定や事象の予測、シミュレーションが可能になります。
回帰分析の基本的な目的は、説明変数と従属変数の関係を関数の形でモデル化することです。
単回帰分析と重回帰分析
- 単回帰分析: 説明変数が1つの場合の回帰分析です。例えば、飲食店のビールの売上(y)とその日の最高気温(x)の関係を調べる場合、単回帰分析を用いて y=ax+c という一次関数の形で表現します。
- この関係が分かると、天気予報を元に仕入れ量を調整することが可能です。
- 重回帰分析: 説明変数が複数ある場合の回帰分析です。
- 例えば、ビールの売上と天気に加え、降水量(z)も考慮する場合、重回帰分析を用いて y=ax+bz+c という形で表現します。
- これにより、より精度の高い予測が可能になります。
線形回帰と非線形回帰
線形回帰
線形回帰は、説明変数と従属変数の関係が直線的な比例関係で表されると仮定する手法です。
一般的には、回帰式は一次関数の形を取ります。
例えば、売上と気温の関係を y=ax+c としてモデル化するのがこれに該当します。
非線形回帰

回帰分析の計算方法
最小二乗法
回帰分析では、データ点と回帰直線との距離が最小になるように係数を決定します。
これを「最小二乗法」と呼びます。
具体的には、各データ点の実際の値と回帰式から得られる予測値との誤差を二乗し、その合計を最小化するように係数を推定します。
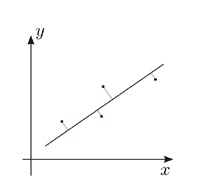
係数の推定
最小二乗法を用いることで、回帰式の係数(傾きや切片)を推定します。
これにより、回帰直線や曲線がデータに最もよく適合するように調整されます。
結果として、データのトレンドをより正確に把握することができます。
実際の応用
ビジネス分野
回帰分析は、ビジネスにおいても非常に役立ちます。
例えば、売上予測、マーケティング効果の分析、リスク管理などで活用されます。
データに基づいた意思決定を行う際に、回帰分析は強力なツールとなります。
科学研究
科学研究においても回帰分析は重要な役割を果たします。
実験データの解析、理論モデルとの適合性の評価、予測モデルの構築などで使用されます。
まとめ
回帰分析は、データの関係性を明らかにし、予測やシミュレーションを行うための基本的な手法です。
単回帰分析や重回帰分析、線形回帰、非線形回帰といった多様な手法を使い分けることで、さまざまなデータに対応できます。
最小二乗法による係数の推定を通じて、データのトレンドを正確に把握し、ビジネスや科学研究での意思決定をサポートします。
回帰分析の理解を深めることで、データの活用方法がさらに広がります。
さらに参考してください。
