対数(logarithm)は、数学やIT分野で頻繁に使用される重要な概念です。
対数を理解することで、指数計算やデータ分析、アルゴリズムの効率化に役立ちます。
本記事では、対数の基本的な仕組みから、日常的な応用例まで詳しく解説します。
対数の計算方法を学ぶことで、複雑な計算を簡単に解くヒントを得ることができます。
対数の基本概念
対数とは?
対数(logarithm)とは、ある数を何乗すると指定の数になるかを表す指数のことです。
具体的には、数値bをa乗すると結果がpになる(b^a = p)場合、この指数aを「bを底とするpの対数」と呼びます。
例えば、2の3乗は8になるので、対数として表すと「log₂8 = 3」です。
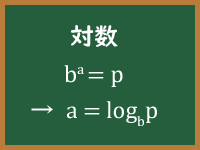
対数の記法と用語
- 底(てい): 対数の基準となる数(例: log₂8 の 2)
- 真数(しんすう): 対数計算の対象となる数(例: log₂8 の 8)
- 指数(しすう): 対数計算によって求められる数(例: log₂8 の 3)
対数の基本公式
対数にはいくつかの基本的な性質があり、これらを理解することで計算が容易になります。
例えば、次の公式が成り立ちます。
- 積の対数: log_b(XY) = log_bX + log_bY
- 商の対数: log_b(X/Y) = log_bX – log_bY
- 冪の対数: log_b(X^n) = n * log_bX
これらの公式を使うことで、複雑な計算をより簡単に処理することができます。
対数の種類と用途
常用対数(common logarithm)
常用対数とは、底が10の対数であり、通常はlog₁₀と表記します。
日常的な計算や科学的なデータ分析においてよく使用されます。
たとえば、地震の震度を表すリヒタースケールは常用対数に基づいて計算されています。
自然対数(natural logarithm)
自然対数は、ネイピア数(e ≈ 2.718)を底とする対数です。
自然対数は数学や物理学、経済学における微分積分計算で重要な役割を果たします。
一般に、自然対数は**ln(ログナチュラル)**という記号で表します。
バイナリ対数(binary logarithm)
バイナリ対数は、底が2の対数であり、コンピュータ科学で頻繁に使われます。
バイナリ対数はデータ構造の最適化やアルゴリズムの効率分析において重要です。
たとえば、バイナリサーチやビッグオー記法での計算に利用されます。
対数の応用例
情報理論とエントロピー
対数は、情報理論において、エントロピーを計算するために使用されます。
エントロピーは、情報の不確実性やランダム性を測定する指標であり、データ圧縮や暗号化アルゴリズムで活用されます。
データ分析とスケーリング
データ分析において、対数変換を行うことで、大きな値の分布を均一化し、データの視覚化や解析がしやすくなります。
例えば、株価の変動を分析する際に、対数スケールを用いることで、長期間の変動を比較しやすくなります。
アルゴリズムの効率化
バイナリ対数は、アルゴリズムの効率分析において特に重要です。
たとえば、バイナリサーチの時間計算量はO(log₂n)であり、これはデータセットのサイズが増えるごとに対数的に検索時間が増加することを意味します。
こうした特性により、大規模データの高速検索が可能になります。
対数計算の例
例1: 常用対数の計算
1000の常用対数を計算する場合:
- log₁₀1000 = 3 (10を3回掛けると1000)
例2: 自然対数の計算
e²の自然対数を求める場合:
- ln(e²) = 2 (eを2乗すると約7.389になる)
例3: バイナリ対数の応用
1024のバイナリ対数を計算する場合:
- log₂1024 = 10 (2を10乗すると1024)
まとめ
対数(logarithm)は、指数計算の逆操作として、数学やコンピュータ科学において非常に重要な役割を果たします。
常用対数、自然対数、バイナリ対数の3種類は、それぞれ異なる分野で有用であり、対数の基本的な性質を理解することで、データ解析やアルゴリズム設計がより効率的になります。
