最小二乗法(Least Squares Method)は、データ分析や統計モデリングにおいて広く利用される手法です。
この手法は、実際のデータと理論モデルの誤差を最小化することで、データ間の関係を明らかにします。
特に、回帰分析やデータフィッティングにおいて不可欠な技術であり、科学、工学、経済学などさまざまな分野で応用されています。
本記事では、最小二乗法の基本概念、実施手順、具体例を詳しく解説します。
最小二乗法の基本概念
最小二乗法とは?
最小二乗法は、与えられたデータ系列 (x1,y1),(x2,y2),…,(xn,yn) の関係をモデル関数 y=f(x) で表現する際、実測値と理論値の誤差の2乗の合計を最小にする方法です。
この手法は、データのばらつきを捉え、最適なフィッティングを提供します。
残差とその最小化
モデル関数の値 f(x1)f(x_1)f(x1) と実際の値 y1y_1y1 の誤差は「残差」と呼ばれ、次のように表されます:
残差=y1−f(x1)この残差を全データにわたって合計し、その2乗を取ることで、残差平方和を計算します。
最小二乗法の目的は、この残差平方和を最小化することです。
最小二乗法の実施手順
ステップ1: モデル関数の選定
最初に、データに適したモデル関数を選定します。
直線的な関係が期待される場合は、一次関数 y=ax+b を用いることが一般的です。
ステップ2: 残差平方和の定義
残差平方和は以下のように表されます:
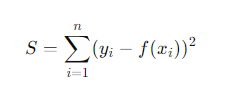
ここで、S は残差平方和で、n はデータ点の数です。
ステップ3: 係数の計算
具体的な解法は選定したモデルによって異なりますが、一次関数の場合、次のように計算します:

最小二乗法の応用例

例: 経済データの分析
ある企業の売上データと広告費用データがあるとします。
このデータを用いて、広告費用が売上に与える影響を分析するために、最小二乗法を用いた線形回帰モデルを構築します。
これにより、広告費用を増加させることで予測される売上の変化を定量化できます。
例: 科学実験のデータフィッティング
実験データを解析する際、最小二乗法を使用して得られた回帰式は、将来の予測や他の実験条件下での結果を推定するための基盤となります。
まとめ
最小二乗法は、データ分析やモデル化において非常に重要な手法であり、実際のデータと理論モデルの誤差を最小化することによって、データ間の関係を明らかにします。
この手法を理解し適用することで、様々な分野でのデータ分析の精度を向上させることが可能です。
最小二乗法の適切な使用は、科学研究やビジネス戦略の決定において強力な武器となります。
