正規分布(ノーマル分布)は、統計学において最も基本的で重要な確率分布の一つです。
この分布は、自然界や社会現象に広く見られるもので、データが平均付近に集中し、平均から離れるにつれて頻度が指数的に減少する特性を持っています。
この記事では、正規分布の基本概念、特性、及びその応用について詳しく解説します。
正規分布の概要
正規分布とは
正規分布(normal distribution)は、データが平均値を中心に対称的に分布し、平均から離れるにつれて確率が急激に減少する確率分布です。
グラフに表すと、「ベルカーブ」と呼ばれる釣り鐘型の形状をしています。自然現象や社会現象に多く見られる分布で、例えば身長、体重、試験の点数などがこの分布に従うことが多いです。
- 平均値、中央値、最頻値が一致: 正規分布は左右対称で、これらの値が同一になります。
- ベルカーブ: グラフは、平均付近が大きく膨らんだ釣り鐘型の曲線になります。
正規分布の確率密度関数

- 平均値 (μ): 分布の中心。
- 標準偏差 (σ): データのばらつき具合を示す。
標準正規分布
正規分布を標準化することで得られるのが標準正規分布です。
標準正規分布では、平均が0、標準偏差が1に調整されます。
この分布を用いることで、異なる正規分布間での比較が容易になります。
正規分布の重要な性質
確率の一定性
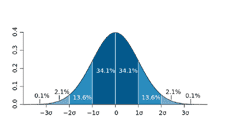
正規分布の特性として、標準偏差の倍数で表される区間にデータが含まれる確率が常に一定である点が挙げられます。
具体的には次の通りです:
- 平均±1標準偏差 (μ±σ) に含まれる確率は約68.27%
- 平均±2標準偏差 (μ±2σ) に含まれる確率は約95.45%
- 平均±3標準偏差 (μ±3σ) に含まれる確率は約99.73%
これらの値は、データのばらつきを理解する上で非常に有用です。
正規分布の応用
正規分布は、多くの実世界の問題をモデル化する際に利用されます。
以下はその一部の例です:
- 品質管理: 製品の品質が正規分布に従うことを仮定し、品質管理の基準を設定します。
- 金融リスク管理: 投資のリスクを評価するために、株価や収益率の分布が正規分布に従うと仮定することがあります。
- 教育統計: テストの点数が正規分布に従うと仮定し、パフォーマンスの分析や比較を行います。
まとめ
正規分布は、データが平均値を中心に対称的に分布し、平均から離れるにつれて頻度が減少する基本的な確率分布です。
その特性により、さまざまな分野で広く応用されています。
正規分布の理解は、統計学やデータ分析を行う上で非常に重要です。
この記事を通じて、正規分布の基本概念やその応用方法について理解を深めていただければ幸いです。
さらに参考してください。
カウンタとは?プログラミングから電子回路、Webまでの全貌を徹底解説
Visited 14 times, 1 visit(s) today
