**深さ優先探索（DFS）**は、グラフや木構造を効率的に探索するための重要なアルゴリズムです。
この手法は、行き止まりのノードに到達するまで進み続け、その後経路を遡って未探索のノードに移動することで、すべてのノードを網羅的に訪問します。
本記事では、深さ優先探索の仕組み、実装方法、及び応用例について詳しく解説します。
深さ優先探索の基本概念
1. DFSの概要
**深さ優先探索（DFS）**は、ノードの探索を進める際に、隣接ノードへ進む方式で、最も最近に追加されたノードから探索を開始します。
この手法は、木構造やグラフにおいて、あるノードから出発し、そのノードに接続されているノードを深く掘り下げていくことが特徴です。
2. DFSの動作原理
深さ優先探索のアルゴリズムは次のように動作します：
- スタートノードから探索を開始します。
- まだ探索していない隣接ノードに移動します。
- 行き止まり（末端ノード）に到達するまで進み続けます。
- 行き止まりに到達したら、経路を遡り、次の未探索ノードに移動します。
- このプロセスを繰り返し、すべてのノードを探索します。
このアルゴリズムは**LIFO（Last-In First-Out）**の原則に基づいており、スタック（stack）というデータ構造を使用して探索候補ノードを管理します。
再帰的な関数呼び出しを用いることで、簡潔に実装することができます。
深さ優先探索の実装
1. プログラム例
以下は、深さ優先探索を再帰的に実装したPythonの例です：
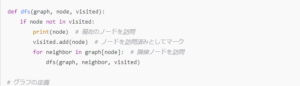
2. 深さ優先探索の特性
深さ優先探索は、広範囲にわたるデータを扱う際に特に有用です。
探索するノードが多い場合でも、記憶領域を効率的に使用でき、再帰的なアプローチにより実装が簡素化されます。
深さ優先探索の応用
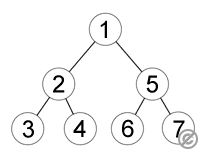
深さ優先探索は、以下のような多くの分野で利用されています：
- パズル解法：迷路やゲームの解決策を見つけるために使用されます。
- トポロジカルソート：依存関係のあるタスクを処理する順序を決定します。
- ネットワーク解析：ネットワークの接続性や構造を理解するための分析に役立ちます。
まとめ
**深さ優先探索（DFS）**は、グラフや木構造を効率的に探索するためのアルゴリズムで、再帰的なアプローチにより簡潔な実装が可能です。
LIFOの原則に基づくこの手法は、多くの実用的なアプリケーションにおいて不可欠です。
深さ優先探索の理解を深めることで、データ構造やアルゴリズムに関する知識が一層豊かになります。
さらに参考してください。
WAU（週間アクティブユーザー）：サービス成功の鍵を握る指標
Visited 1 times, 1 visit(s) today