相加平均(算術平均)は、複数の値から求める平均値の一つであり、一般的には「平均」や「平均値」と呼ばれることが多いです。
本記事では、相加平均の計算方法やその特徴、他の平均値との違いについて詳しく解説し、統計やデータ分析における重要性を強調します。
相加平均の基本概念
1. 相加平均とは
相加平均は、与えられた数値を単純に加算し、その合計を値の個数で割った結果として求められます。
例えば、数値の集合が {10, 20, 30} の場合、その相加平均は次のように計算されます:
相加平均=(10+20+30)3=20\text{相加平均} = \frac{(10 + 20 + 30)}{3} = 20
このように、相加平均はデータの集計や分析において最も一般的に使用される代表値です。
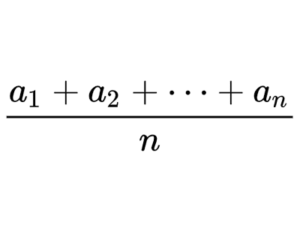
2. 相加平均の計算方法
相加平均を計算する際の手順は以下の通りです:
- 値の加算:全ての値を足し合わせる。
- 個数で割る:合計値を値の個数で割る。
この方法は非常にシンプルで、多くの場面で利用されます。
3. 他の平均値との比較
相加平均には他にもいくつかの平均の計算方法があります。以下はその代表的なものです:
- 相乗平均(幾何平均):すべての値を掛け合わせ、そのn乗根を取ります。
相加平均に比べ、極端な値に影響されにくい特性があります。
- 調和平均:値の逆数の相加平均を求め、その逆数を取ります。
特に、速度や比率の計算に適しています。
4. 統計における平均値の意義
統計の分野では、相加平均以外にも「中央値」(データを順位で並べた際の真ん中の値)や「最頻値」(最も多く現れる値)など、他の代表値も考慮されます。
データの特性に応じて適切な平均値を選ぶことが重要です。
相加平均の注意点
相加平均は、少数の極端な値に強く影響を受ける特性があります。
このため、データセットに外れ値が存在する場合、相加平均だけではデータの代表値として適切でない場合があります。
そのため、平均値の選択には注意が必要です。
まとめ
相加平均(算術平均)は、複数の値から平均値を求めるための基本的かつ重要な手法です。
その計算方法はシンプルで、データ分析や統計の分野で広く利用されています。
他の平均値との違いを理解し、データの特性に応じて適切な代表値を選ぶことが、分析の精度を高めるために不可欠です。
