調和平均（harmonic mean）とは？データ解析における重要な平均値の一つ

**調和平均（harmonic mean）**は、統計学やデータ解析において非常に重要な役割を果たす平均値の一つです。

特に、速度や比率の平均を求める際に非常に効果的です。

本記事では、調和平均の定義、計算方法、他の平均との違い、具体的な応用例について詳しく解説します。

調和平均の基本概念

1. 調和平均とは

調和平均は、与えられた数値の逆数の相加平均を求め、その逆数を取ることによって計算されます。

この平均値は、特に速度や比率を扱う場合に使用されることが多いです。

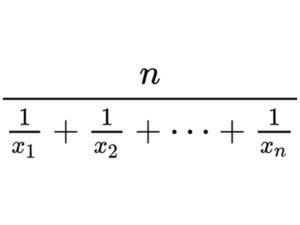
2. 調和平均の計算方法

調和平均を求める際の手順は以下の通りです：

• 複数の数値を用意します。例として、{20, 30}という2つの値を考えます。
• 各値の逆数を求めます。具体的には、1/20と1/30です。
• これらの逆数を足し合わせ、その合計を値の個数で割ります。調和平均=n(1×1+1×2+…+1xn)\text{調和平均} = \frac{n}{\left(\frac{1}{x_1} + \frac{1}{x_2} + … + \frac{1}{x_n}\right)}調和平均=(x1​1​+x2​1​+…+xn​1​)n​ここで、$n$は値の個数、xix_ixi​は各値を示します。この例の場合、調和平均は約24となります。

3. 他の平均との違い

調和平均は、他の平均（相加平均や相乗平均）と異なる特性を持ちます：

• 相加平均（算術平均）：全ての値を足し合わせ、その合計を値の個数で割ります。
• 相乗平均（幾何平均）：全ての値を乗算し、その値の個数に対する累乗根を取ります。

調和平均は、特に比率や速度のように相対的な関係が重要なデータにおいて有効です。

調和平均の応用例

1. 速度の計算

調和平均は、異なる速度で移動する際の平均速度を求める場合に非常に有用です。

例えば、ある距離を異なる速度で移動した際の平均速度を計算することができます。

2. 統計解析

調和平均は、データセットにおける極端な値の影響を受けにくいため、特定の状況下での代表値として利用されます。

特に、比率が重要視される経済学や社会科学の分野で重宝されています。

まとめ

**調和平均（harmonic mean）**は、データ解析や統計学において重要な平均値の一つです。

特に、速度や比率の計算において有用であり、他の平均値との違いを理解することで、より正確なデータ分析が可能になります。

調和平均を適切に活用することで、データの特性をより正確に捉えることができるでしょう。

さらに参照してください：

QAM（Quadrature Amplitude Modulation）とは？デジタルデータ伝送の革新技術