論理否定(NOT演算)は、論理演算の中でも最も基本的かつ重要な概念です。
与えられた条件や命題が真(true)であれば偽(false)に、偽であれば真に反転させる演算であり、プログラミング、電子工学、コンピュータアーキテクチャにおいて広く使用されています。
この記事では、論理否定の原理・記号・論理回路としての役割・プログラミング言語における実装などを詳しく解説し、実務への応用例も紹介します。
論理否定(NOT演算)とは?
論理否定の基本概念
論理否定とは、ある命題や条件の真偽値を反転させる演算です。
-
入力が 真(true) → 出力は 偽(false)
-
入力が 偽(false) → 出力は 真(true)
これは単項演算子(Unary Operator)に分類され、1つのオペランド(被演算子)に対して適用されます。
真理値表で見るNOT演算
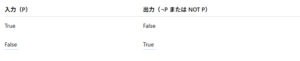
このように、真理値を逆にするのが論理否定です。
論理否定の記号と表記法
論理学における表記
論理学では以下のような記号が使われます:
-
¬P(Pを否定する)
-
または ~P, NOT P と書かれることもあります。
電子工学・論理回路での表記
電子回路設計では、オーバーライン(上線)やインバータ記号を使用して表します:
-
例:P̅(Pにオーバーラインを付けて表す)
-
「NOTゲート」または「インバータ」という名称の基本論理回路として実装されます。
プログラミングにおける論理否定の使用法
主要言語での記法一覧
さまざまなプログラミング言語で論理否定は異なる表記を持ちます:
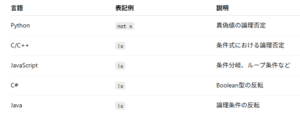
ビット演算におけるNOT(ビット反転)
ビット単位の論理否定(ビット反転)もよく使われます:
-
C言語などでは
~xと表記され、すべてのビットを反転します。-
例:
~0b1010→0b0101
-
-
用途:フラグ操作、ビットマスク、符号の反転 など
NOTゲートと論理回路における役割
NOTゲート(インバータ)とは
NOTゲートは、単一入力を反転して出力する基本的な論理回路素子です。
デジタル回路設計において、以下のように活用されます:
-
入力が HIGH(1) → 出力は LOW(0)
-
入力が LOW(0) → 出力は HIGH(1)
回路内での使用例
-
制御信号の反転:例:有効/無効フラグの切り替え
-
AND/ORゲートと組み合わせた複合論理:NANDやNOR回路の構成に使用
-
クロック反転・エッジ制御など、タイミング制御にも活用
実用例と注意点
条件式での論理否定

このように、「~でない場合」という表現で多用されます。
ビット反転の例(C言語)

ビットマスクとしての応用、ネガティブ値の生成などに使用されます。
注意点
-
論理否定とビット否定の混同に注意
-
データ型によって
!や~の意味が変わることがある(特にC/C++) -
Boolean値以外の型に使う場合、暗黙的な型変換に注意が必要
まとめ
論理否定(NOT演算)は、あらゆるプログラミングや電子回路の設計において基本でありながら応用範囲が広い概念です。
-
真偽値やビットの反転を1つのオペランドで実行
-
記号:¬,
!,~,notなどが言語や分野で使い分けられる -
NOTゲートは論理回路における不可欠な基本素子
-
多くのプログラミング言語で条件分岐やビット操作に応用されている
この知識をしっかりと理解することで、バグの少ないコードの設計や効率的なハードウェア制御が可能になります。
ITエンジニアとしての基礎力を高めるためにも、論理否定の理解は欠かせません。
