比例尺度(ratio scale)は、統計学やデータ分析、さらにIT領域のアルゴリズム開発において、データの性質を理解し、適切に処理するための重要な概念です。
単に数値があるだけでは適切な分析はできません。「その数値にどんな意味があるか?」を判断するために、「尺度水準」という考え方があり、その中で比例尺度は最も情報量が多く、すべての統計手法が使用可能な強力なスケールです。
この記事では、比例尺度の定義、特徴、具体例、他の尺度との違い、ITにおける実用例を専門的に解説します。
比例尺度とは?
尺度水準の中で最も情報量の多い分類
比例尺度は、1946年にアメリカの心理学者スタンレー・スティーブンズが提唱した「4つの尺度水準(名義尺度・順序尺度・間隔尺度・比例尺度)」の中で最も高い水準に位置します。
この尺度の特徴は以下の3点です:
-
数値が順序性と間隔性を持つ
-
**絶対的なゼロ点(0 = 存在しない)**がある
-
数値同士で比率や割合の比較が可能
この性質により、加減乗除を含むすべての数学的・統計的演算が可能になります。
比例尺度の具体的な例
以下のようなデータは、すべて比例尺度に該当します:
-
長さ(cm、mなど)
-
重さ(kg、g)
-
時間(秒、分、時)
-
金額(円、ドル)
-
個数(整数値)
-
絶対温度(ケルビン)
比較例:摂氏温度と絶対温度

このように、0の意味の有無が「間隔尺度」と「比例尺度」の違いです。
IT分野における比例尺度の活用例
1. データベース設計
売上金額、在庫数量、処理時間などのカラムは、すべて比例尺度に該当します。
これにより、SQL上での集計(SUM, AVG, MAX, MIN)や、BIツールでのグラフ化が可能です。
![]()
2. 機械学習における特徴量(Feature)
線形回帰やロジスティック回帰など、多くのアルゴリズムでは数値の意味が重要です。
比例尺度の特徴量であれば、そのままモデルに投入でき、重み付けや正規化も意味を持ちます。
例:
-
入力変数:処理時間(秒)、ファイルサイズ(MB)、アクセス件数
-
出力変数:サーバ負荷率(%)
3. パフォーマンスモニタリング
-
APIのレスポンスタイム
-
CPU使用時間
-
スループット(1秒あたりの処理数)
これらはすべて比例尺度であり、過去データと比較することで「2倍遅くなった」「50%改善された」など、定量的に評価が可能です。
他の尺度との比較
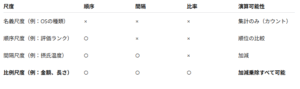
比例尺度を利用した統計手法
比例尺度は、すべての統計手法を適用可能です:
-
平均、中央値、最頻値
-
分散、標準偏差
-
相関係数、回帰分析
-
分散分析(ANOVA)
また、グラフでの表現(折れ線グラフ、棒グラフ、散布図など)にも適しており、視覚的にも説得力のあるデータ分析が可能になります。
まとめ
比例尺度(ratio scale)は、以下のような特長を持ち、データサイエンスやIT分野の基盤となる重要な概念です:
-
数値に順序・間隔・比率の意味があり、数学的・統計的な処理がすべて可能
-
実世界の多くの物理量やビジネスデータは比例尺度として扱われる
-
他の尺度(名義・順序・間隔)よりも情報量が多く、分析の自由度が高い
データ分析や機械学習に取り組む際、まず「このデータは比例尺度かどうか」を意識することで、正しい処理・解釈・結果導出が行えるようになります。
今後の統計解析やシステム設計で、比例尺度の概念を意識的に取り入れることが、精度の高い意思決定や品質の高いソフトウェア開発につながるでしょう。
