バブルソート(Bubble Sort)は、もっとも基本的で古典的なソート(整列)アルゴリズムの一つです。
教育や入門に頻繁に登場する一方で、実務ではあまり用いられない傾向もありますが、アルゴリズムの設計・評価・最適化の観点から非常に重要な位置づけにあります。
本記事では、バブルソートの仕組み、計算量、メリット・デメリット、最適化、実用性までを、ITエンジニア向けに詳しく解説します。
バブルソートの基本構造
バブルソートとは?
バブルソートは、与えられた配列内の隣接要素を比較して交換する操作を繰り返すことで、配列を整列状態にするアルゴリズムです。
処理の流れ(基本アルゴリズム)
-
配列の先頭から末尾に向かって、隣り合う2つの要素を比較
-
並べたい順序と逆であれば交換
-
末尾まで処理したら1回の「パス」が完了
-
必要な回数(最大 n−1)繰り返すことで、すべての要素が整列される
📌 各パスの末尾には最大(または最小)の要素が確定し、「泡のように浮かび上がる」様子からバブルソートと名付けられました。
バブルソートの擬似コード(例:昇順)

バブルソートの特徴とパフォーマンス
計算量(時間計算量)
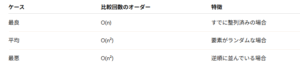
空間計算量
-
O(1)(インプレースソート):追加の記憶領域が不要
安定性
-
安定ソート:同じ値の要素の相対順序が保たれる
バブルソートの実用性と使用シーン
メリット
-
実装が非常に簡単で、アルゴリズムの理解に適している
-
安定ソートであり、内部ソート(in-place)である
-
並列化しやすい構造を持つ(全ての比較・交換操作が独立している)
デメリット
-
計算量が大きく、大規模データには不向き
-
実用的な場面ではより高速なアルゴリズム(クイックソート、マージソートなど)に取って代わられている
主な用途
-
アルゴリズム学習教材として(基本の整列アルゴリズムの理解)
-
小規模かつ特定条件下での使用(例えば、ほとんど整列されているデータの最終確認など)
バブルソートの最適化と派生手法
最適化1:交換フラグによる早期終了
整列済みの配列に対して無駄なパスを実行しないために、交換が1回も起きなかったら処理を終了する実装。

最適化2:未整列範囲の縮小
各パスで最後に交換された位置より後はすでに整列されているため、次回のパスではその位置までしか比較しないように調整可能。
派生アルゴリズム
-
シェーカーソート(カクテルソート):双方向にパスを行うことで効率化
-
コンブソート(Comb Sort):比較対象の距離を変化させることで高速化
-
奇偶ソート(Odd–Even Sort):並列処理に適した改良型
他のソートアルゴリズムとの比較
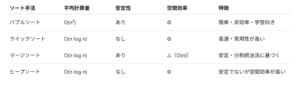
まとめ
バブルソート(Bubble Sort)は、最も基本的な整列アルゴリズムの一つであり、簡単に実装でき、安定かつインプレースな特徴を持ちます。
ただし、大規模データに対しては非効率であり、主に教育・学習用途で活用されます。
-
基本原理:隣接要素を比較・交換
-
計算量:O(n²)、ただし最良ケースはO(n)
-
適用範囲:学習用、小規模データ、並列処理の基礎理解
アルゴリズムの入門において、バブルソートをしっかり理解することは、他のソート手法の理解にもつながります。
まずはここから始めて、より高度なアルゴリズムへと進みましょう。
