倍精度浮動小数点数(double precision real number)は、科学技術計算や3Dグラフィックス、機械学習など、精度が重要な分野で幅広く利用されている数値表現形式です。
この記事では、倍精度浮動小数点数の基本的な構造や利点、単精度・半精度との違い、実際のIT現場での応用例までを詳しく解説します。
倍精度浮動小数点数とは?
倍精度浮動小数点数の定義
倍精度浮動小数点数とは、64ビットのデータを使用して実数を表現する浮動小数点数の一種であり、「double」として多くのプログラミング言語で使用されているデータ型です。
この形式は、実数を仮数部(mantissa)と指数部(exponent)に分けて表現し、高い精度を保ちながら広い範囲の数値を扱うことができます。
IEEE 754 標準に基づく内部構造
現在主流となっているIEEE 754標準では、倍精度浮動小数点数は以下のように構成されています:
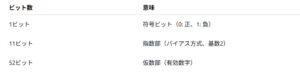
この構造により、表現できる値の範囲はおよそ 2.2×10⁻³⁰⁸ 〜 1.8×10³⁰⁸ であり、有効数字は約16桁にも達します。
他の浮動小数点数との比較

倍精度が活用される実際のシーン
科学技術計算(シミュレーション)
物理シミュレーションや気象モデルなど、極めて微細な変化を追跡する必要がある場面では、丸め誤差が致命的な影響を与えることがあります。
そのため、倍精度が標準的に利用されます。
機械学習とAI分野
機械学習では通常、訓練時は倍精度または単精度が使われ、推論時には半精度を使うケースが増えています。
倍精度の使用は、モデルの安定性や学習精度の向上につながることがあります。
金融計算・統計解析
為替レートの計算や保険モデルのシミュレーションなど、わずかな数値誤差が大きな損失に繋がる分野では、倍精度の重要性が非常に高いです。
倍精度のメリットとデメリット
メリット
-
高い精度で計算でき、丸め誤差が少ない
-
広範囲の値を扱える
-
IEEE 754標準により互換性と信頼性が高い
デメリット
-
メモリ使用量が大きい(64ビット)
-
処理速度が単精度に比べて遅くなる場合がある
まとめ
倍精度浮動小数点数(double precision real number)は、高精度な数値計算が求められる分野で欠かせない存在です。
その64ビット構造によって、高精度かつ広い数値範囲を実現しており、現代のIT技術の根幹を支えています。
IEEE 754準拠のフォーマットにより、多くのプログラミング言語やハードウェアで広く採用されており、科学、金融、AIといった最先端領域での活用が進んでいます。
今後、さらに高精度・高速化が求められる分野では、この倍精度表現の理解がより重要になっていくでしょう。
