半加算器(half adder)は、デジタル回路設計において最も基本的な加算回路のひとつであり、2つのビットの加算を実現するための重要な構成要素です。
この記事では、半加算器の仕組み、全加算器との違い、さらには実際の論理回路設計での使い方や構成方法について、IT技術者の視点から詳しく解説します。
デジタル回路やコンピュータアーキテクチャの学習において、確実に理解しておきたい基本概念です。
半加算器の概要
半加算器とは?
半加算器(half adder)は、2進数の1ビット同士の加算を行う論理回路です。
特徴として、下位桁からの繰り上がり(キャリー入力)を考慮しない点が挙げられます。
つまり、最下位ビットの加算処理など、限定的な用途に適したシンプルな加算器です。
この回路は、入力される2ビット(通常はAとB)に対して、以下の2つの出力を生成します:
-
合計ビット(Sum)
-
キャリービット(Carry out)
例:2ビット加算の出力例
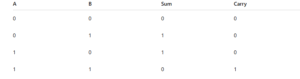
このように、AとBが両方1の場合は、合計として「10」(2進数)が出力され、Sum = 0、Carry = 1となります。
論理回路における構成
基本構成と使用ゲート
半加算器は論理ゲート(AND、OR、XOR、NOTなど)を用いて構成されます。
代表的な構成には以下の2通りがあります。
1. XOR + AND構成(推奨)
-
Sum(合計):A XOR B
-
Carry(繰り上がり):A AND B
この構成では、XOR回路が利用可能な場合、最も簡潔で効率的に実装できます。
2. 基本ゲートのみで構成
XOR回路がない場合は、以下のように複数の論理ゲートを組み合わせることでもXOR相当の動作を再現可能です:
-
XOR = (A AND (NOT B)) OR ((NOT A) AND B)
-
Carry = A AND B
このようにして、最小限の論理回路でも半加算器を構築することが可能です。
全加算器との違いと関係
全加算器(full adder)との違い
全加算器(full adder)は、半加算器の拡張版です。
違いは、以下の点にあります:
-
全加算器は、3つの入力(A, B, Carry in)を加算する
-
半加算器は2つの入力(A, B)のみ
つまり、全加算器は「前の桁からの繰り上がり(Carry in)」を受け取り、それを加味して出力を生成します。
半加算器2つで全加算器を構成する
1つの全加算器は、2つの半加算器と1つのORゲートで構成可能です。
以下はその接続例です:
-
半加算器1:A + B → 中間Sum, 中間Carry
-
半加算器2:中間Sum + Carry in → 出力Sum
-
ORゲート:中間Carry + 半加算器2のCarry → 出力Carry
このように、半加算器は全加算器の基本構成要素としても非常に重要です。
半加算器の応用例
実際の利用シーン
-
算術論理演算ユニット(ALU)の構成要素として
-
CPU内部の加算回路の一部に
-
組み込み機器のシンプルな加算演算に
教育・学習分野での活用
回路設計やデジタル論理の基本を学ぶ教材としても、半加算器はよく取り上げられます。
論理ゲートの理解と実装スキルの習得に適しており、初学者が回路設計の仕組みを理解するための出発点とも言えます。
まとめ
半加算器(half adder)は、デジタル回路における基本的な加算ロジックを実現するシンプルな論理回路です。
繰り上がりを考慮しないため、最下位ビットの加算や全加算器の構成要素として用いられます。
XORとANDの基本ゲートを使って簡潔に実装でき、全加算器との組み合わせにより多ビットの加算処理が可能になります。
デジタル回路設計やコンピュータアーキテクチャの基礎理解において、必ず押さえておきたい重要なキーワードです。
