回帰直線(regression line)は、データ分析や統計学において重要な役割を果たすツールです。
特に、二つの変数間の関係を視覚的に示し、予測や推測を行うための基礎となります。
本記事では、回帰直線の基本的な概念から、最小二乗法の計算手法までを詳しく解説し、その実際の応用例を紹介します。
回帰直線とは?
基本概念

ここで、x は説明変数、y は目的変数です。
この直線を用いることで、既知のデータから未知の値を予測することが可能になります。
回帰直線の描画
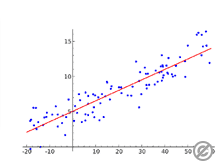
回帰直線は、横軸に説明変数、縦軸に目的変数を取った散布図上に描画されます。
回帰分析を用いて得られるこの直線は、実際のデータ点との距離が最小になるように調整されます。
直線の傾き(a)と切片(b)は、データの分布に基づいて最適化されます。
最小二乗法による計算
最小二乗法の目的
回帰直線を決定するためには、最小二乗法が広く使用されます。
この方法は、実際のデータ点と回帰直線との距離の二乗和を最小化することを目的としています。
この距離の二乗和を「残差平方和」と呼びます。
残差平方和の計算
![]()
係数の求め方

実際の応用
ビジネス分野での利用
回帰直線は、ビジネス分野での予測や傾向分析に広く用いられています。
例えば、売上高と広告費用の関係を分析する際に回帰直線を使うことで、将来の売上を予測することができます。
科学研究での利用
科学研究でも回帰直線は重要な役割を果たします。
実験データの傾向を把握し、理論モデルとの適合性を評価するために用いられます。
まとめ
回帰直線は、データ分析において変数間の関係を視覚的に表現し、予測や分析を行うための強力なツールです。
最小二乗法を用いることで、回帰直線の係数を精確に求めることができ、ビジネスや科学研究など様々な分野での応用が可能です。
データ分析における基礎的な知識を深めるために、回帰直線の理解と利用は欠かせません。
さらに参考してください。
