幅優先探索(Breadth-First Search:BFS)は、グラフ構造や木構造を探索する基本的かつ重要なアルゴリズムの一つです。
プログラミングやアルゴリズムの学習において、DFS(深さ優先探索)と並んで頻出のテーマであり、ネットワーク解析・ルート探索・人工知能など幅広い分野で活用されています。
この記事では、BFSの仕組み・特徴・実装方法や実用的な活用例まで詳しく解説します。
幅優先探索(BFS)とは?
幅優先探索の基本概念
幅優先探索(BFS)は、探索を開始するノード(頂点)から距離の近いノードを順番に広がるように探索する手法です。
具体的には、次のような順序でノードを辿ります:
-
最初に探索するノードの隣接ノード(距離1)をすべて探索
-
次に、その隣接ノードの隣接ノード(距離2)を探索
-
この操作をノード全体が探索されるまで繰り返す
このように、BFSでは同じ距離にあるノードを一括で処理するため、あるノードから最短経路を見つけるのに非常に適しています。
キュー(Queue)とFIFO方式
探索順序の管理に使われるデータ構造
BFSの重要な特徴は、「先に追加したノードから順に探索する」という点です。
これはFIFO(First-In First-Out)方式と呼ばれ、探索の候補ノードの順序を正しく保つためにキュー(queue)というデータ構造が使用されます。
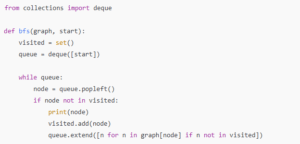
上記のPythonコードは、隣接リストで表現されたグラフに対してBFSを行う簡単な例です。
dequeは高速なキュー操作を可能にし、visitedセットで再訪問を防ぎます。
幅優先探索の具体的な応用例
1. 最短経路の探索(無加重グラフ)
BFSは、すべてのエッジに同じコストがかかる無加重グラフにおいて、最短経路を見つけるために非常に有効です。たとえば:
-
地図上の道のり(例:最短の道順)
-
ソーシャルネットワークにおける最短の人間関係
2. レベル構造の解析
ツリー構造でBFSを使うことで、各ノードの深さ(レベル)を効率的に取得することができます。
これは、構文解析やツリーデータの表示構成(UI)などに活用されます。
3. AIにおける状態空間探索
ゲームAIやパズル解法などで、状態空間を浅い順から広げて探索するのにBFSは理想的です。
特に、解の最短手順が求められる場面で有効です。
幅優先探索と深さ優先探索の違い

まとめ
幅優先探索(BFS)は、グラフや木構造において距離の近いノードから順に探索する効率的なアルゴリズムです。FIFO方式で処理順を制御し、キュー(queue)を用いることが最大の特徴です。特に最短経路の探索や状態空間の幅広い探索においてその真価を発揮します。
アルゴリズムを扱う際には、DFSとBFSの特性を正しく理解し、用途に応じて使い分けることがITエンジニアとして重要なスキルとなります。
プログラム実装や演習問題を通して、ぜひBFSの理解を深めてみてください。
