平衡木(Balanced Tree)は、アルゴリズムやデータベース設計、ソフトウェアエンジニアリングなどの分野で非常に重要な木構造(ツリー構造)の一種です。
データの探索や挿入、削除などを効率的に実行できるよう最適化された構造であり、大量のデータを扱う現代のITシステムにおいて欠かせない要素です。
この記事では、平衡木の基本概念から具体的な種類、活用例までを詳しく解説します。
平衡木の基本概念
木構造とは?
まず、木構造とは、親ノードが複数の子ノードを持つことができるというルールで構成された階層型のデータ構造です。
最上位にあるノードを根ノード(ルート)、末端にあるノードを葉ノード(リーフ)と呼びます。
この構造において、根から各葉までの距離(ノードを何回経由するか)を「深さ(または高さ)」と呼びます。
平衡木の定義
平衡木とは、どの葉ノードに至る経路の深さがなるべく等しくなるように設計された木構造です。
ノードの追加や削除が行われた際には、自動的に再構成(リバランス)され、バランスが保たれます。
これにより、最悪ケースの深さが抑制されるため、探索や挿入・削除といった操作における計算量(時間効率)が向上します。
平衡木の代表的な種類と特徴
平衡二分木(Balanced Binary Tree)
定義
二分木(Binary Tree)とは、各ノードが最大2つの子ノードを持つ木構造です。
これを平衡に保つことで、探索などの処理が平均 O(log n) の時間で実行可能になります。
例:AVL木・赤黒木
-
AVL木(AVL Tree):各ノードの左右の部分木の高さ差が1以内であることを条件とする。
挿入や削除時に回転操作で再バランス。
-
赤黒木(Red-Black Tree):各ノードに赤または黒の属性を持たせることで、全体のバランスを保つ。
実装がやや複雑だが、再バランス処理が効率的。
平衡二分探索木(Balanced Binary Search Tree)
これは、平衡二分木に二分探索の条件(左 < 親 < 右)を加えたもの。
代表的な用途としては、辞書構造やデータベースの索引処理があります。
B木(Bツリー)およびその派生構造
特徴
-
各ノードが複数の子ノードを持てる「多分木」形式。
-
ディスクアクセス最適化を目的とし、データベースやファイルシステムにおいて主に使用される。
-
子ノード数やキーの数に制限があり、階層を浅く保てるため大規模データでも効率的。
派生構造
-
B+木:すべてのデータが葉に格納され、リーフ同士が連結された構造。
レンジクエリが効率的。
-
B*木:B木よりも高いデータ密度を持ち、ノード分割の頻度が低下。
平衡木の活用例
データベース管理システム(DBMS)
インデックス構造としてのB木やB+木は、数百万件のレコードでも高速な検索・更新を可能にします。
メモリ管理・スケジューラ
OSのメモリ管理アルゴリズムやプロセススケジューリングでは、AVL木や赤黒木が使われることが多く、リアルタイム性が要求される処理に有効です。
ソート・検索アルゴリズム
探索効率の高い平衡二分探索木は、検索対象のデータが事前にわかっている場合に効率的な探索アルゴリズムの中核として機能します。
平衡木と非平衡木の性能比較
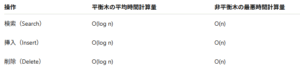
このように、平衡木の採用によりアルゴリズムの性能が大きく向上することがわかります。
まとめ
-
平衡木(balanced tree)は、データ構造として安定した探索性能を提供し、大規模データ処理に不可欠です。
-
代表例としては平衡二分木、AVL木、赤黒木、B木、B+木などがあり、それぞれ異なる目的に最適化されています。
-
探索や挿入、削除処理の効率を保つための再構成(バランシング)が自動で行われる点が特徴です。
-
OS、データベース、検索アルゴリズムなど、ITインフラの中核に多く活用されています。
