散布図（スキャッターダイアグラム）とは？データ分析における強力なツール

**散布図（scatter diagram）**は、データ分析において重要な視覚化手法の一つです。

本記事では、散布図の定義、作成方法、そしてその分析手法について詳しく解説します。

特に、データの関係性や傾向を把握するために散布図を活用する方法を学ぶことは、IT業界やデータサイエンスの専門家にとって極めて重要です。

散布図の基本概念

散布図とは？

散布図は、異なる特性や量の間の関係を明らかにするために使用されるグラフです。

通常、縦軸と横軸には異なる特性が割り当てられ、各データポイントはこれらの特性に基づいて配置されます。

点がどのように分布するかを観察することで、二つの量の間に関連があるかどうかを判断できます。

散布図の作成方法

1. データの準備: 分析したい二つの特性や量のデータを収集します。
2. 軸の設定: 縦軸に一方の特性、横軸にもう一方の特性を設定します。
3. データポイントのプロット: 各データポイントを対応する位置にプロットします。

散布図の解釈

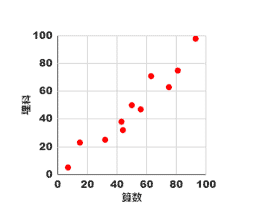
• 正の相関: 点が右上がりの帯状に分布している場合、二つの量には正の相関があります。
• 負の相関: 左上から右下に向かって点が分布している場合は、負の相関が示されます。
• 相関なし: 点がまんべんなく散らばっている場合、二つの量の間には関連性が薄いと考えられます。

散布図の利点と応用

特異点の特定

散布図は、データ全体の傾向から大きく外れた**特異点（外れ値）**を容易に特定できます。

これにより、外れ値を除外したり、その原因を調査したりすることが可能です。

グルーピング

また、散布図を使用して、データポイントの集まり具合から二つの量の関係が同じ傾向を示す項目群をグループ分けすることもできます。

これにより、データをより深く分析し、有意義なインサイトを得ることができます。

具体例

例えば、企業のマーケティングデータを分析する際に、広告費と売上高の関係を散布図で可視化することができます。

この分析により、広告投資が売上に与える影響を明確に理解でき、今後の戦略を立てるための根拠を得ることが可能になります。

まとめ

**散布図（スキャッターダイアグラム）**は、データ分析における強力な視覚化ツールであり、二つの特性の関係性を明らかにするのに非常に有効です。

正の相関、負の相関、または相関がないかを判断することで、データの洞察を深め、ビジネスや研究における意思決定をサポートします。

データサイエンスやITの分野での応用を理解し、散布図を効果的に活用することで、より良い結果を導き出すことができるでしょう。