木構造(Tree Structure)は、データの階層的な配置を表現するための基本的なデータ構造です。
本記事では、木構造の基本的な概念から、さまざまな木構造の種類やその実装方法について詳しく解説します。
木構造は、データの整理や検索、管理において非常に重要な役割を果たしており、理解することでより効率的なデータ処理が可能になります。
木構造の基本概念
木構造とは?
木構造は、データを階層的に整理するためのデータ構造で、次の要素から構成されます:
- ノード(Node):木構造の基本要素で、データや情報を格納します。
- エッジ(Edge):ノード同士の接続を表します。
木構造では、ノードが親子関係を持ち、各ノードは複数の子ノードを持つことができます。
根ノード(Root Node)は木の最上部にあり、親ノード(Parent Node)と子ノード(Child Node)という階層を形成します。
ノードの種類と関係
- 根ノード(Root Node):木構造の最上部に位置し、親ノードを持たないノードです。
- 親ノード(Parent Node):子ノードを持つノードで、他のノードの親となります。
- 子ノード(Child Node):親ノードから分岐するノードです。
- 葉ノード(Leaf Node):子ノードを持たないノードで、木の末端に位置します。
- 枝ノード(Branch Node):子ノードを持つノードで、内部ノードとも呼ばれます。
ノードの深さ(Depth)と高さ(Height)は、木構造の特徴を表す重要な要素です:
- 深さ(Depth):根ノードから特定のノードまでのエッジの数です。
- 根ノードの深さは0です。
- 高さ(Height):特定のノードから、その子孫の葉ノードまでのエッジの数です。
- 木全体の高さは根ノードの高さです。
木構造の分類
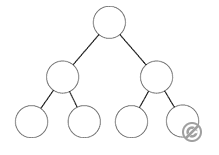
二分木(Binary Tree)
二分木(Binary Tree)は、各ノードが最大2つの子ノードを持つ木構造です。
二分木は、簡単な実装と効率的な検索性能から、広く使用されています。
例えば、二分探索木(Binary Search Tree)は、データの検索を効率的に行うために設計された二分木です。
多分木(Multi-way Tree)
多分木(Multi-way Tree)は、各ノードが3つ以上の子ノードを持つことができる木構造です。
一般的に、子ノードの数に制限がなく、多くの値を格納することができます。
代表的な多分木には、B木(B-Tree)やB+木(B+ Tree)があります。
N分木(N-ary Tree)
N分木(N-ary Tree)は、親ノードが最大N個の子ノードを持つ木構造です。
Nが2の場合は二分木、Nが3以上の場合は三分木や四分木などと呼ばれます。
N分木には以下の種類があります:
- 全N分木(Full N-ary Tree):すべてのノードがN個の子ノードを持つ木です。
- 完全N分木(Perfect N-ary Tree):すべての葉ノードが同じ深さにあり、完全に埋められた木です。
- 完全N分木(Complete N-ary Tree):すべての階層が満たされ、最下層のノードができるだけ左に寄せられた木です。
木構造の応用
木構造は、さまざまな実際のアプリケーションで使用されています。
例えば、ファイルシステムのディレクトリ構造や、家系図、ゲームのAIなど、階層的なデータを扱う際に非常に有効です。
また、データベースのインデックスや、ネットワークトラフィックの管理にも応用されます。
まとめ
木構造(Tree Structure)は、データを階層的に整理するための強力なデータ構造です。
ノード、エッジ、根ノード、葉ノードなどの基本概念を理解し、二分木、多分木、N分木などの種類と応用方法を把握することで、データ管理や検索、分析が効率的に行えます。
木構造の特性を活かし、さまざまな場面で効果的なデータ処理を実現しましょう。
さらに参考してください。
