**木構造(tree structure)**は、データ構造の一つで、情報を階層的に整理するために用いられます。
この構造は、親ノードが複数の子ノードを持ち、さらにそれらの子ノードが孫ノードを持つという形で分岐していく特性があります。
木構造は、データの効率的な管理と検索を可能にし、多くのITシステムやアプリケーションで使用されています。
本記事では、木構造の基本概念、構成要素、種類、そしてその応用について詳しく解説します。
木構造の基本概念
木構造とは?
木構造は、ノード(node)とエッジ(edge)から成り立つデータ構造です。
ノードは情報の単位であり、エッジはノード間のつながりを示します。
木構造の最上部に位置するノードを**根ノード(root node)**と呼び、親ノードと子ノードの関係が形成されます。
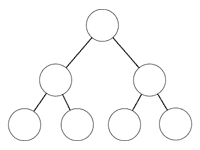
木構造の構成要素
- ノード(node): 情報を保持する基本単位。
- エッジ(edge): ノード間の関係を示す接続線。
- 親ノード(parent node): 他のノードを子ノードとして持つノード。
- 子ノード(child node): 親ノードから直接つながっているノード。
- 葉ノード(leaf node): 子ノードを持たない最終的なノード。
木構造の特性
木構造は、深さ(depth)、高さ(height)、幅(width)という特性を持っています。
- 深さ: 根ノードから特定のノードまでのエッジの数。
- 高さ: 特定のノードから最も深い葉ノードまでのエッジの数。
- 幅: 同じ深さにあるノードの数。
木構造の種類
二分木(Binary Tree)
二分木は、各ノードが最大で2つの子ノードを持つ木構造です。
この構造は、効率的なデータの検索やソートを実現するために広く使用されます。
多分木(Multi-Branch Tree)
多分木は、各親ノードが3つ以上の子ノードを持つことができる木構造です。
特定の数以下の子を持つ「N分木」としても知られています。
例えば、3つ以下の子ノードを持つ場合は「三分木」、4つ以下は「四分木」と呼ばれます。
平衡木(Balanced Tree)
平衡木は、すべての葉ノードの深さができるだけ等しくなるように構築された木です。
特に、検索効率が求められるデータベースシステムでよく使用されます。
木構造の応用
データベース管理
木構造は、データベースのインデックスを構成するために用いられ、効率的なデータ検索を可能にします。
B木やB+木などの平衡木は、特に大規模データベースで広く使用されています。
コンピュータプログラミング
プログラミングにおいては、木構造がさまざまなアルゴリズムの基礎として使用されます。
例えば、木構造を利用した探索アルゴリズムは、データの管理や処理において非常に重要です。
組織構造の可視化
企業や団体の組織図を木構造で表現することで、階層的な関係を視覚的に理解しやすくなります。
この形式は、情報の整理やコミュニケーションの効率化に寄与します。
まとめ
**木構造(tree structure)**は、データの効率的な管理と検索を実現するための基本的なデータ構造です。
ノードとエッジから成り立ち、階層的な情報の整理が可能であり、二分木や多分木、平衡木などの種類が存在します。
IT分野において、木構造はデータベース管理やプログラミング、組織構造の可視化など、多岐にわたって応用されています。
この構造の理解は、データ管理における効率を高めるために不可欠です。
