**標本化定理(sampling theorem)**は、アナログ信号をデジタル信号に正確に変換するための基礎的な理論です。
この定理は、信号の最大周波数の2倍のサンプリング周波数でサンプリングを行えば、元の信号を忠実に再現できることを示しています。
本記事では、標本化定理の詳細、重要性、具体的な応用について深く掘り下げていきます。
標本化定理の基本
標本化定理とは?
標本化定理は、アナログ信号をデジタル化する際に重要な概念です。
この定理によれば、アナログ信号に含まれる最大周波数の2倍以上のサンプリング周波数でサンプリングを行うことで、元の信号を正確に再構成できることが保証されます。
これにより、デジタル信号から元のアナログ信号の波形を忠実に復元することが可能になります。
サンプリングのプロセス
アナログ信号をデジタル信号に変換するためには、以下のプロセスが必要です:
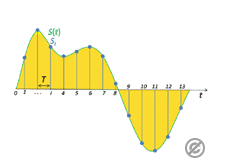
- サンプリング: 一定の周期で信号の振幅を測定します。
- 量子化: 測定値を離散的な数値に変換します。
このサンプリング周期が短いほど、サンプリング周波数が高くなり、元の波形をより正確に記録できますが、同時に生成されるデータ量も増加します。
標本化定理の重要性
信号再構成の精度
標本化定理の核心は、信号の再構成精度にあります。
サンプリング周波数が元の信号の最大周波数の2倍以上であれば、デジタル信号から正確にアナログ信号を復元できるとされています。
これは、デジタル信号がサンプリング周波数の半分の周波数までの信号を正確に再現できることを意味します。
この半分の周波数を**ナイキスト周波数(Nyquist frequency)**と呼びます。
アプリケーションにおける影響
標本化定理は、音声処理や画像処理などの分野において非常に重要です。
例えば、音楽CDは44.1kHzでサンプリングされており、これにより20kHzまでの音を忠実に再現することができます。
このように、適切なサンプリング周波数の選定は、音質や画像品質に直接影響を与えます。
標本化定理の応用例
音声処理
音声処理において、標本化定理は音質の向上に寄与しています。
サンプリング周波数が高いほど、音声信号の細部まで正確に再現できます。
例えば、44.1kHzでサンプリングされた音楽データは、人間の聴覚範囲をカバーし、クリアな音質を提供します。
画像処理
画像処理においても、標本化定理が重要です。画像をデジタル化する際、ピクセルのサンプリング周波数を適切に設定することで、解像度を向上させることができます。
これにより、画像の詳細が保持され、より鮮明な表示が可能になります。
まとめ
本記事では、標本化定理について詳しく説明しました。
この定理は、アナログ信号をデジタル信号に変換する際の重要な指針であり、信号の忠実な再現を実現します。
特に音声や画像処理の分野において、その影響は計り知れません。
適切なサンプリング周波数を選ぶことで、質の高いデジタルデータを得ることができるため、この理論を理解することは非常に重要です。
さらに参考してください。
