相加平均(算術平均)は、データ分析や統計の分野で非常に重要な概念です。
この平均値は、複数の数値を単純に加算し、その合計を数値の個数で割ることで求められます。
本記事では、相加平均の定義や計算方法、他の平均との違い、そしてデータ分析における応用について詳しく解説します。
相加平均の定義と計算方法
1. 相加平均とは
相加平均は、あるデータセットの代表値として広く用いられています。
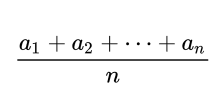
具体的には、数値の集合が与えられた場合、それらの数値をすべて加算し、その合計をデータの個数で割った値を指します。
この方法は最も一般的な平均値の計算方法です。
1.1 計算方法の例
例えば、データセット {10, 20, 30} の相加平均を計算する場合:
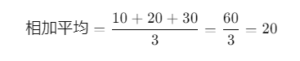
このように、相加平均は簡単に求めることができ、多くの場面で利用されます。
2. 相加平均の応用
相加平均は、データの集計や分析において非常に有用です。
特に、社会調査や経済指標の分析などで、特定の集団や現象の代表値を求める際に活用されます。
他の平均との比較
1. 相乗平均
相乗平均(幾何平均)は、全ての値を掛け合わせて n 乗根を取ることで求められます。
相加平均が数値の和を利用するのに対し、相乗平均は数値の積を基にした代表値です。
2. 調和平均
調和平均は、各数値の逆数を使い、その相加平均を求めてから再度逆数を取ることで算出されます。
特に、速度や効率の計算において重要な指標です。
3. 中央値と最頻値
統計においては、相加平均以外にも中央値(median)や最頻値(mode)などの代表値があります。
中央値はデータを順序付けた際の中央の値、最頻値は最も頻繁に出現する値を示します。
これらは特にデータに極端な値が存在する場合において、相加平均よりも実情に即した代表値となることがあります。
相加平均の注意点
相加平均を使用する際には、少数の極端な値(外れ値)の影響を受けやすいことに注意が必要です。
例えば、データセットに非常に大きな数値が含まれていると、相加平均はその影響を強く受け、実際のデータの代表値として適切でなくなることがあります。
まとめ
本記事では、相加平均の基本的な概念や計算方法、他の平均との違い、データ分析における重要性について詳しく説明しました。
相加平均は、データを効果的に要約し、理解するための強力なツールです。
この知識を活用することで、より適切なデータ分析を行い、価値ある洞察を得ることができるでしょう。
さらに参考してください。
