主成分分析（PCA）とは？データ解析の強力なツールを徹底解説

主成分分析（PCA）は、統計学の多変量解析手法として非常に重要な役割を果たしています。

本記事では、PCAの基本的な概念やその応用について詳しく解説します。

特に、次元削減や相関関係の発見といったPCAの特性を理解することで、データ解析における効率性を高めることができます。

主成分分析（PCA）の概要

PCAとは？

主成分分析（PCA）は、多数の説明変数から相関のある組み合わせを見つけ出し、これを一つの合成変数に置き換える手法です。

この方法により、データの次元を圧縮し、解析モデルを単純化することが可能です。

例えば、複数の科目のテスト結果からデータモデルを構築する際に、各科目の得点をそのまま用いると、高次元になりすぎて分析が困難になります。

PCAのプロセス

PCAは以下のようなプロセスで実行されます：

1. 相関関係の特定
   例えば、数学の得点（Sm）と物理の得点（Sp）が強く相関している場合、これを以下のように合成します：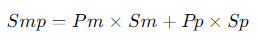
   ここで、Smpは第1主成分、PmとPpは相関を最大化するように計算されます。
2. 他の主成分の発見
   第1主成分と直交する他の変数の組み合わせを見つけ出します。

たとえば、国語と英語の得点を合成して第2主成分とします。

3.次元の削減
このプロセスを繰り返し、変数の数を削減していきます。

主成分が3変数以上の合成になることもあり、その解釈が難しい場合もあります。

固有値と寄与率

主成分に含まれる情報の量は「固有値」で表され、各主成分がデータ全体のどの程度を説明できるかは「寄与率」と呼ばれます。

第1主成分から第n主成分までの寄与率を累積したものを「累積寄与率」といい、実用上は80%以上の累積寄与率に達した時点で残りの主成分は無視することが一般的です。

PCAの実用例

データ解析への応用

PCAは多くの分野で応用されています。

例えば、以下のようなシナリオがあります：

• 画像処理: 高解像度画像のデータを圧縮し、情報を保持しつつデータ量を減らす。
• 金融分析: 複数の経済指標からのデータを統合して、リスク管理や投資判断を行う。
• 医療データ: 患者の検査結果から主要な因子を抽出し、診断の精度を向上させる。

まとめ

主成分分析（PCA）は、多変量解析において非常に強力なツールです。

データの次元削減や相関関係の発見を通じて、解析の効率を大幅に向上させることができます。

本記事で紹介した基本的なプロセスや応用例を理解することで、PCAの実用的な価値を実感できるでしょう。

データ解析において、PCAの重要性を再認識し、適切に活用していきましょう。