バックトラック法(Backtracking Method)は、組み合わせや探索問題において、すべての可能性を検討しつつ、不要なパターンを早期に排除することで効率よく解を見つけるアルゴリズムです。
探索空間が膨大になるような問題において計算量を抑え、IT分野のアルゴリズム設計で頻繁に使われます。
本記事では、バックトラック法の基本原理、実装例、代表的な適用ケースなどを詳しく解説します。
バックトラック法の概要
バックトラック法とは?
バックトラック法とは、条件に合致する解を探す過程で、一部の候補が最終的な解にならないと判明した時点で、その探索を中止し、直前の状態に戻って他の選択肢を試す探索アルゴリズムです。
この「引き返し(backtrack)」の動作によって、全探索(brute-force)より効率的に問題を解決できます。
バックトラック法の仕組みと特徴
探索の基本ステップ
-
問題の解を構成するための部分解を一つずつ仮定
-
途中でその部分解が不適切(条件を満たさない)と判明した場合は、その道を放棄して別の選択肢へ
-
条件を満たす解をすべて列挙、または一つでも見つかれば終了する(用途により異なる)
効率化のポイント
-
明らかに条件を満たさない部分解を早期に排除(枝刈り(pruning))
-
部分的な検証で全体の計算コストを削減
バックトラック法の実用例
具体的な問題への適用
パズルやゲームの解法
-
数独(Sudoku):各セルに数字を仮定しながら矛盾があれば引き返す
-
ナイトの巡回問題:全てのマスをナイトで一度だけ踏む巡回ルートを探索
-
Nクイーン問題:チェス盤に互いに攻撃しないようにN個のクイーンを配置する
組み合わせ列挙
例:サイコロA, B, Cの目の合計が10以上になるすべてのパターンを探す問題
-
全探索では 6×6×6 = 216通り
-
バックトラック法を使えば、不要な分岐(例:A=1, B=1の時点でCが何でも10未満)をスキップできる
→ 検証回数を大幅に削減
ファイル構造探索や経路問題
-
ディレクトリ再帰検索
-
迷路探索や経路復元
バックトラック法の実装と注意点
実装の基本構造(擬似コード)
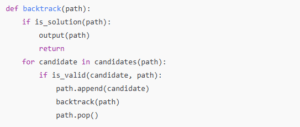
実装時の注意点
-
スタックの管理:再帰処理で深い探索になるため、スタックオーバーフローに注意
-
ループの最適化:候補の絞り込みを行うことで処理時間を短縮
-
状態のキャッシュ:同じ状態を再評価しないようメモ化を検討
バックトラック法と他の探索法の比較

まとめ
バックトラック法(Backtracking Method)は、探索空間が膨大な組み合わせ問題において非常に有効なアルゴリズムです。
覚えておくべきポイント:
-
不適切な部分解は早期に排除(枝刈り)し、処理効率を向上
-
全探索よりも計算量が削減され、特に条件付きの問題に強い
-
ゲーム、AI、数理最適化など幅広いIT分野で応用
今後のプログラム開発やアルゴリズム選定において、バックトラック法の理解と活用は必須のスキルとなります。
