カルノー図(Karnaugh map)は、論理式を簡略化するための強力なツールです。
この図を使うことで、複雑な論理式を視覚的に整理し、より短い形式で表現することが可能になります。
本記事では、カルノー図の基本的な概念、構造、及びその利点を詳しく解説します。
カルノー図の基本概念
定義と歴史
カルノー図は、1953年にアメリカのベル研究所のモーリス・カルノーによって提案されたもので、元々はベイチ図(Veitch diagram)の改良版です。
論理式の各変数の入力値と対応する出力値を整理することで、論理回路の設計を効率化します。
目的
カルノー図の主な目的は、冗長な部分を削減し、必要な素子の数を減らしながら同じ機能を持つ回路を設計することです。
これにより、コスト削減や動作速度の向上が期待できます。
カルノー図の構造
2次元のマス目
カルノー図は、通常、縦横に並んだマス目の形式で表現されます。
最上段と左端には各変数の入力値(「0」と「1」の組み合わせ)を列挙し、それ以外のマスには対応する論理式の出力値が記載されます。
一般的には、「1」の場合のみを書き入れ、空欄は「0」とみなします。
変数の数に応じた構造
- 2変数: 2×2の表
- 3変数: 2×4または4×2の表
- 4変数: 4×4の表
- 5変数: 4×8または8×4の表
通常、次元あたり2変数、全体で4変数までが扱われます。
これ以上の次元を扱うと、簡略化が難しくなります。
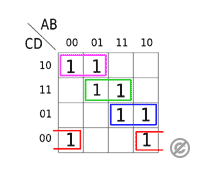
カルノー図の利点
視覚的な簡略化
カルノー図は、論理式を視覚的に整理できるため、複雑な論理関係を直感的に理解しやすくします。
たとえば、複数の「1」を隣接させてグループ化することで、共通部分を見つけやすくなります。
効率的な設計
冗長な回路を排除することで、回路設計の効率を高めます。
たとえば、デジタル回路の設計において、カルノー図を使用することで最適なゲート数を導き出すことができます。
実際の使用例
カルノー図は、デジタル論理回路の設計だけでなく、ソフトウェア開発や信号処理など、さまざまな分野で応用されています。
たとえば、デジタル回路の論理ゲートを最適化する際に、カルノー図を使ってシンプルな表現に変換することができます。
まとめ
カルノー図は、論理式を簡略化するための強力なツールであり、視覚的な整理を通じて冗長な部分を削減します。これにより、効率的な回路設計が可能となり、さまざまな分野での応用が期待できます。
論理式の簡略化を目指す際は、カルノー図を活用することで、より最適な解決策を見つける手助けとなるでしょう。
さらに参考してください。
