再帰関数とは、関数がその定義の中で自身を呼び出す特性を持つ関数のことを指します。
この特性により、特定の計算や処理をシンプルに表現することが可能になります。
本記事では、再帰関数の基本的な概念、使用例、注意点について詳しく解説します。
再帰の理解は、効率的なアルゴリズムを設計する上で非常に重要です。
再帰関数の基本概念
再帰関数の定義
再帰関数は、自己呼び出しを含む関数です。このような関数は、計算や処理を繰り返す際に非常に便利です。
例えば、階乗の計算やフィボナッチ数列の計算は、再帰的な定義に基づいて実装できます。
- 階乗の計算：
n!=n×(n−1)!n! = n \times (n-1)! - フィボナッチ数列の計算：
F(n)=F(n−1)+F(n−2)F(n) = F(n-1) + F(n-2)
再帰呼び出しの重要性
再帰関数では、内部で「再帰呼び出し」（recursive call）が行われます。
このプロセスは、問題を小さな部分に分けて解決する際に役立ちます。
多くのプログラミング言語では、再帰関数を使って複雑なロジックをシンプルに表現することができます。
再帰関数の実装方法
実装の例
以下は、Pythonでの再帰関数の実装例です。
このコードでは、階乗とフィボナッチ数列を計算するための再帰関数を定義しています。
factorial関数では、0の場合の基底条件を設定し、それ以外の場合は再帰的に自身を呼び出します。
同様に、fibonacci関数も基底条件を持ち、再帰的に計算を行います。
リエントラント構造の重要性
再帰関数を記述する際には、関数が無限に呼び出されないように、適切な脱出条件を設けることが重要です。
脱出条件が欠けていると、無限ループに陥り、最終的にはスタックオーバーフローが発生します。
このため、再帰関数は「リエントラント」な構造である必要があります。
リエントラントな関数は、内部状態が壊れないように設計されています。
再帰関数の応用
再帰関数は、特にデータ構造やアルゴリズムの設計において多くの応用が見られます。
以下は、その一部です。
1. データ構造の探索
再帰を用いたアルゴリズムは、ツリーやグラフなどのデータ構造の探索に利用されます。
特に、深さ優先探索（DFS）は再帰的な手法を用いることが一般的です。
2. ソートアルゴリズム
クイックソートやマージソートなどのソートアルゴリズムも、再帰を用いて実装されることが多いです。
これらのアルゴリズムは、配列を小さな部分に分割し、それぞれを再帰的にソートします。
まとめ
再帰関数（recursive function）は、自己呼び出しを特徴とする関数であり、効率的なアルゴリズムを設計するために不可欠な技術です。
正しく実装することで、複雑な問題をシンプルに解決することが可能になります。
再帰の理解を深めることで、プログラミングスキルを向上させることができるでしょう。
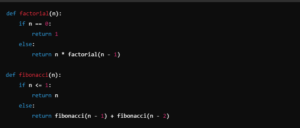
さらに参考してください。
