再帰処理（Recursion）の基本と実践的活用法

再帰処理とは、プログラムの実行中にその処理自身を再び呼び出し、処理を繰り返すことを指します。

この技法は特に、複雑なデータ構造を扱う際や、反復的な計算を行う際に非常に有効です。

本記事では、再帰処理の基本概念、実装方法、及びその具体的な利用例について詳しく解説します。

再帰処理の基本概念

再帰処理とは

再帰処理は、ある関数が自身を呼び出すプロセスを含んでいます。

これにより、問題を小さな部分に分割し、同様の処理を繰り返すことが可能になります。

再帰処理を実装するためには、まず以下の要素を理解する必要があります。

• 再帰関数：自身を呼び出すコードを含む関数。
• ベースケース：再帰の終了条件。無限ループを避けるために必要です。
• 再帰ケース：問題を小さく分解するための条件。

再帰関数の実装

再帰関数は、一般的に次のような形で実装されます：

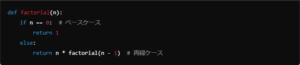
この例では、階乗（n!）を計算するための再帰関数を定義しています。

nが0の場合は1を返し、それ以外の場合はnとn-1の階乗の積を返します。

再帰処理の応用

階層的データの処理

再帰処理は、特に階層的なデータ構造を扱う際に非常に役立ちます。

たとえば、ツリー構造のデータを走査する場合、再帰を使用して各ノードを訪れることができます。

例：ツリーの深さ優先探索

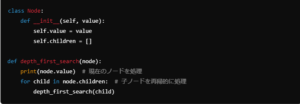
この例では、各ノードの値を出力する深さ優先探索を実装しています。

再帰処理によって、各ノードの子ノードを簡潔に走査できます。

再帰処理の利点と注意点

• 利点:
  • 複雑な処理をシンプルなコードで表現できる。
  • 階層構造のデータを容易に扱える。
• 注意点:
  • 無限ループに陥るリスクがあるため、適切なベースケースを設定することが重要。
  • 再帰の深さが深くなると、スタックオーバーフローを引き起こす可能性がある。

まとめ

再帰処理は、プログラムにおける強力な手法であり、特に複雑なデータ構造や計算に対して効果的です。

再帰関数を理解し、正しく実装することで、より効率的なプログラムを作成することができます。

再帰処理の適切な利用は、プログラミングのスキルを一段と向上させるでしょう。

さらに参考してください。

再帰問い合わせ（Recursive DNS Query）の基本と仕組み