標準偏差(Standard Deviation / SD) は、統計学やデータ分析において最も重要な指標の一つです。
特にIT分野、例えば機械学習、AI、品質管理、システムパフォーマンス分析など、様々な応用領域で活用されています。
本記事では、「標準偏差とは何か」を基礎から丁寧に解説し、数式だけでなく、実用例やプログラムへの応用方法も紹介します。
エンジニアやデータサイエンティストにとっての実務的な活用視点から、理解を深めましょう。
標準偏差とは何か?統計の基本を理解する
データのばらつきを表す指標
標準偏差(SD) とは、データの平均からのズレの平均的な大きさを示す指標です。
標準偏差が小さい場合は、データが平均値の近くに集中しており、逆に大きい場合は、平均値から離れたデータが多いことを意味します。
つまり、標準偏差は「安定性」や「信頼性」を数値化するものとも言えます。
計算方法(数式)
標準偏差は次のような手順で求められます:
-
データの平均値を計算する
-
各データと平均値の差を2乗する
-
その合計をデータ数で割り、分散を求める
-
分散の平方根を取ることで、標準偏差が得られる
式で表すと以下の通りです:
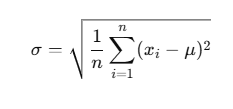

実例で学ぶ:標準偏差の理解を深める
具体例①:データが均等に離れている場合

→ 中央の値にある程度集中している状態。
具体例②:より広く分布している場合

→ 同じ平均値でも、ばらつきが大きくなると標準偏差も増加します。
具体例③:すべて同じ値の場合

→ すべてのデータが平均と等しいため、ばらつきがない。
標準偏差のIT分野での応用
1. 機械学習とデータ前処理
標準化(Zスコア正規化) では、標準偏差を用いて各データを同じスケールに変換します:
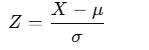
これにより、異なる単位や桁数のデータでも、機械学習モデルに適した形に整えられます。
2. 品質管理(QC)
製造業などでは、製品の寸法や性能のばらつきを数値化するために標準偏差が使われます。
これにより、品質の一貫性や改善余地を評価できます。
3. システムパフォーマンス分析
Webサーバーの応答時間、APIのレイテンシ、ユーザーの操作時間などの変動を分析する際、標準偏差が役立ちます。
平均応答時間が同じでも、標準偏差が大きければユーザー体験は不安定になる可能性があります。
4. 学力評価(偏差値)
日本の教育分野では、テストの結果を比較可能にするために偏差値を使います。
これは標準偏差を基に算出され、個人の得点が集団の中でどの位置にあるかを示す指標です。
分散との違いと使い分け
分散は標準偏差の前段階となる指標ですが、単位が元データの単位と異なるため、実用的には標準偏差の方が比較や解釈に適しています。
例えば、データが「秒」であれば、分散は「秒の二乗」、標準偏差は「秒」となり、直感的に扱いやすいのは後者です。
まとめ
標準偏差(SD)は、単なる数学的な指標にとどまらず、IT分野のさまざまな実務に直結する重要な概念です。
特に以下の点を押さえておきましょう:
-
標準偏差はデータの散らばり具合を表す
-
平均からのズレを数値化することで、信頼性や安定性の判断が可能
-
データ分析・AI・品質管理・教育評価など多分野で活用されている
標準偏差を理解し使いこなすことは、高度なデータ処理スキルの基盤となります。
エンジニア、アナリスト、教育関係者にとって必須の知識といえるでしょう。
