オーダー記法(ランダウの記号は、アルゴリズムの計算量を評価する際に使用される重要な概念です。
IT分野で効率的なプログラムを作成するためには、この記法を理解することが欠かせません。
本記事では、オーダー記法の基本から、どのようにアルゴリズムの性能を評価するかについて詳しく解説します。
オーダー記法の基本概念
オーダー記法とは?
オーダー記法は、関数の極限における値の変化を評価するための記法です。
特に、アルゴリズムの計算量を大まかに表す際に利用されます。例えば、関数 f(x) = x^2 + x + 1 において、x が無限大に向かって増加すると、第1項 x^2 が最も影響を持つため、他の項は無視されます。
これを記号 O(ビッグオー) を使って f(x) = O(x^2) と表現します。
計算量のオーダー
アルゴリズムの計算量を評価する際、最も影響の大きな項を残し、それ以外の項や定数の係数は無視されます。
これにより、入力データが増加するにつれて、アルゴリズムの計算量がどのように増加するかを大まかに把握できます。
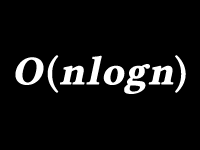
計算量オーダーの種類
定数時間 O(1)
定数時間 O(1) のアルゴリズムは、入力データの量に関わらず一定の時間で処理が完了します。
例えば、配列の特定の位置にある要素を取得する操作は O(1) です。
対数時間 O(log n)
対数時間 O(log n) のアルゴリズムは、データ量 n の対数に比例して計算時間が増加します。
バイナリサーチ(2分探索)がこれに該当し、データが増加しても計算時間の増加が抑えられます。
線形時間 O(n)
線形時間 O(n) のアルゴリズムは、データ量 n に正比例して計算時間が増加します。
リスト内のすべての要素を順番に処理する場合などがこれに該当します。
準線形時間 O(n log n)
準線形時間 O(n log n) は、データ量 n とその対数の積に比例します。
高速なソートアルゴリズムであるマージソートやクイックソートが O(n log n) に該当します。
二乗時間 O(n^2)
二乗時間 O(n^2) のアルゴリズムは、データ量の2乗に比例して計算時間が増加します。
2つのリストのすべての組み合わせを比較する操作など、計算量が多くなる場合に使用されます。
多項式時間 O(n^c) と 指数時間 O(k^n)
多項式時間 O(n^c) は、データ量 n の c 乗に比例し、指数時間 O(k^n) は定数 k の n 乗に比例します。
これらのアルゴリズムは、データ量が増加すると非常に急速に計算時間が増加します。
階乗時間 O(n!)
階乗時間 O(n!) のアルゴリズムは、データ量の階乗に比例します。
組み合わせ問題などで見られ、データ量が少し増加するだけで計算時間が爆発的に増加します。
アルゴリズムの性能評価とオーダー記法
最悪・平均・最良の計算時間
アルゴリズムの性能を評価する際、最悪計算時間、平均計算時間、最良計算時間の3つの観点から評価することが重要です。
例えば、クイックソートは平均と最良の計算量が O(n log n) と高速ですが、特定の規則性を持つデータに対しては最悪 O(n^2) となることがあります。
このように、データの特性や最悪ケースを考慮することが必要です。
実際の活用例
アルゴリズムの設計やデータ構造の選択において、計算量オーダーの理解は不可欠です。
例えば、検索やソートの頻度が高いシステムでは、O(n log n) や O(log n) のアルゴリズムを選択することで、システムの効率を大幅に向上させることができます。
また、大規模なデータセットを扱う際には、O(n^2) や O(n!) のアルゴリズムを避けるべきです。
まとめ
オーダー記法(ランダウの記号は、アルゴリズムの計算量を評価し、効率的なプログラムを作成するために不可欠なツールです。
データ量に応じたアルゴリズムの性能を把握し、適切に選択することで、より効率的で高性能なシステムを構築できます。
最悪・平均・最良の計算時間を理解し、さまざまな状況に適したアルゴリズムを選ぶことが、ITエンジニアにとって重要なスキルとなります。
