倍精度浮動小数点数型(double precision floating point number type)は、プログラミングにおいて数値演算を行う際に不可欠なデータ型です。
64ビットの構造により、広い範囲と高い精度を両立しており、科学技術計算、統計分析、グラフィックス処理など、さまざまなIT分野で利用されています。
この記事では、その構造・仕様から、具体的な使用シーン、他の浮動小数点数型との違いまで詳しく解説します。
倍精度浮動小数点数型とは何か?
基本的な定義と特徴
倍精度浮動小数点数型(double型)とは、64ビット長の実数を表すことができるデータ型で、主にC言語やJava、Pythonなど多くのプログラミング言語で採用されています。
可変小数点を扱えるため、整数では表現できない小さな値や非常に大きな値まで幅広く対応できます。
例:
![]()
このように、小数点以下15〜16桁程度の精度で実数を表現できるため、精度が求められる演算に適しています。
IEEE 754規格による構造
倍精度型の表現方式は、広く採用されているIEEE 754 binary64フォーマットに基づいています。
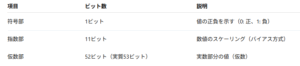
IEEE 754では、仮数の先頭の「1」が正規化により暗黙的に存在するため、実質的に53ビットの精度を実現しています。
これにより、表現できる値の範囲は約 ±1.79769×10³⁰⁸、精度は最大で 15〜16桁 に達します。
他の浮動小数点数型との違い
単精度(float型)との比較
-
単精度(32ビット):精度は約7桁、表現範囲は±3.4×10³⁸
-
倍精度(64ビット):精度は約15桁、表現範囲は±1.8×10³⁰⁸
倍精度はその分メモリ使用量と計算コストが高くなりますが、誤差に敏感なアプリケーションでは不可欠です。
半精度(16ビット)との比較
主にディープラーニングの推論処理など、演算回数が多く、かつ精度がそこまで求められない場合に使われます。
倍精度は、学習フェーズや物理シミュレーションなど高精度が必要な場面に適します。
倍精度型が活躍するIT分野の実例
科学技術計算
気象シミュレーション、粒子物理学、天文学などでは、非常に微小な差を正確に追跡する必要があり、倍精度による計算精度が結果に大きく影響します。
金融工学・統計解析
為替計算、リスク評価、ポートフォリオ最適化など、小数点以下の微差が重要な意思決定に直結するため、double型が広く使用されています。
グラフィックス・3Dモデリング
ゲーム開発やCADでは、複雑な座標計算・ベクトル処理に倍精度を使うことで、精密な描画と演算の安定性を確保します。
まとめ
倍精度浮動小数点数型(double型)は、IT分野における高精度演算を支える重要なデータ型です。
IEEE 754規格に基づいた64ビット構造により、高い精度と広い範囲の数値を表現することが可能です。
用途に応じて、単精度や半精度との使い分けが求められますが、科学技術計算や金融分野、グラフィックスなど、正確性が重視される分野では倍精度が標準となっています。
プログラミングや数値処理を行うすべてのITエンジニアにとって、この倍精度浮動小数点数型の正しい理解は、精度の高いソフトウェア設計の第一歩となるでしょう。
さらに参考してください:
倍精度浮動小数点数とは?―高精度計算を支える64ビットの仕組みを徹底解説
