加算器(アダー)は、2進数の加算を行うための重要な論理回路です。
本記事では、加算器の基本的な構成要素、動作原理、実際の応用例などについて詳しく解説します。
加算器を理解することは、デジタル回路やコンピュータアーキテクチャの基礎を学ぶ上で非常に重要です。
加算器の基本
加算器の種類
加算器は主に以下の2つの種類に分類されます:
- 半加算器(half adder)
- 全加算器(full adder)
これらを組み合わせることで、任意の桁数の加算器を構成することが可能です。
半加算器の動作
半加算器は、2進数の同じ桁のビットを加算し、その結果を出力します。
出力は2つの部分から成り立っています:
- 和(sum):その桁の結果
- キャリー(carry out):次の桁への繰り上がりを示す値
例えば、2つのビットが両方「1」の場合、和は「0」となり、キャリーは「1」となります。
このキャリーは、隣の桁に影響を与えるため、重要な役割を果たします。
全加算器の動作
全加算器は、半加算器を基にしたより複雑な回路で、以下の3つの入力を持ちます:
- 二数の同じ桁のビット
- 下位桁からのキャリー
全加算器は、これらの入力を加算し、次の2つを出力します:
- 和:その桁の結果
- キャリー:次の桁への繰り上がり
全加算器は、2つの半加算器と1つのORゲートで構成されるため、効率的に実装できます。
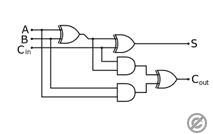
複数桁の加算器の構成
多桁加算器の設計
複数桁の加算器は、最下位桁に半加算器を配置し、上位桁に全加算器を並べることで構成されます。
各加算器のキャリー出力は、上位桁の全加算器の入力に接続されます。
例
例えば、1つの半加算器と7つの全加算器を用いることで、8ビットの加算器を設計することができます。
この構成により、8ビットの2進数を効率的に加算できます。
実際の応用例
加算器は、コンピュータの算術論理ユニット(ALU)やデジタル信号処理(DSP)など、さまざまな分野で広く使われています。
特に、加算器の効率的な設計は、全体のシステム性能に直結します。
まとめ
加算器は、2進数の加算を実現するための基本的な論理回路であり、半加算器と全加算器から構成されます。
加算器を理解することは、デジタル回路やコンピュータアーキテクチャの学習において欠かせないステップです。複数桁の加算器を設計することで、より複雑な計算を行うことができ、実際のアプリケーションにも応用可能です。
加算器の知識を活用し、さらなる技術の習得に繋げていきましょう。
さらに参考してください。
