楕円曲線暗号(ECC: Elliptic Curve Cryptography)**は、楕円曲線上の離散対数問題という数学的難問を基礎とした暗号技術です。
1985年にビクター・ミラー氏とニール・コブリッツ氏によって独立に考案され、以後、**ECDSA(楕円曲線DSA)やECDH(楕円曲線Diffie-Hellman鍵交換)**といったアルゴリズムに応用されています。
本記事では、ECCの基本原理、利点、応用例、そしてRSA暗号との比較を通じて、ECCの魅力に迫ります。
ECCの基本原理
楕円曲線とは?
楕円曲線は次のような方程式で表される数学的曲線です:y2=x3+ax+by^2 = x^3 + ax + b
この曲線上の二点間の座標に対して特殊な加算法が定義されており、点Gを自身に何度も加算することで任意の倍数nGを計算できます。この繰り返しによって生成されたポイント群がECCの基盤を形成します。
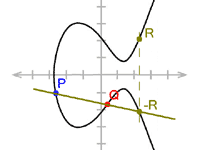
楕円曲線上の離散対数問題(ECDLP)
ECCのセキュリティは、**楕円曲線上の離散対数問題(ECDLP: Elliptic Curve Discrete Logarithm Problem)**に依存しています。
- 簡単な方向:与えられた点Gをn倍して得た点Xを計算するのは容易です。
- 難しい方向:しかし、点XとGから元のスカラー値nを求めることは非常に困難で、効率的な計算手法は発見されていません。
これがECCの強力なセキュリティを支える基盤です。
ECCの利点
1. 短い鍵長で高いセキュリティ
ECCは短い鍵長でRSAなど他の公開鍵暗号方式と同等のセキュリティを提供します。
例えば、256ビットのECC鍵は、3072ビットのRSA鍵と同じレベルのセキュリティを実現できます。
この特性により、データ処理の効率化と通信負荷の軽減が可能です。
2. 計算量の削減
ECCはRSAと比べて暗号化や復号に必要な計算量が少ないため、処理能力の限られたデバイス(例:ICカード、モバイルデバイス)でも優れたパフォーマンスを発揮します。
そのため、IoT機器やスマートデバイスへの採用が進んでいます。
ECCの応用例
楕円曲線DSA(ECDSA)
ECDSAは、ECCの特性を利用したデジタル署名アルゴリズムです。
短い鍵長で強力なセキュリティを提供するため、SSHやTLS、ブロックチェーン技術など、データの整合性確認が重要な場面で広く利用されています。
楕円曲線Diffie-Hellman鍵交換(ECDH)
ECDHは、暗号化通信において安全な鍵交換を行うためのアルゴリズムです。
通信経路上で共通の秘密鍵を生成する際、ECDLPの難解さを活用して盗聴者からの攻撃を防ぎます。
VPNやHTTPS通信において、この技術が用いられています。
暗号通貨のウォレット
暗号通貨(例えばビットコイン)のウォレットでは、ECCを使った鍵ペア(秘密鍵と公開鍵)が生成され、トランザクション署名に利用されています。
この技術により、ユーザーは自分の資産を安全に管理できます。
ECCとRSAの比較
1. 鍵長とセキュリティ
RSAでは3072ビットの鍵が必要なところ、ECCでは256ビットで同様のセキュリティが得られます。
これにより、鍵管理や通信データ量の削減が大幅に簡略化されます。
2. 計算の効率
ECCは、RSAと比較して計算の負荷が軽く、デバイスの消費電力を抑えることが可能です。
そのため、特にモバイルデバイスや組み込みシステムにおいてはECCの方が有利です。
3. セキュリティの将来性
量子コンピュータが登場すると、RSAはその安全性が危ぶまれますが、ECCは量子計算に対してもより強固であるとされています。
今後のセキュリティ対策を考慮すると、ECCは有望な選択肢となります。
ECCの注意点
楕円曲線の選定
ECCの安全性は、使用する楕円曲線のパラメータ設定に大きく依存します。
適切に選ばれた曲線を使用しないと、セキュリティに問題が生じる可能性があります。
ランダム性の確保
ECCで使用するランダム値が予測可能であると、暗号の強度が著しく低下します。
そのため、高品質な乱数生成が必要不可欠です。
まとめ
楕円曲線暗号(ECC)は、RSAに代わる次世代の暗号方式として、短い鍵長で高いセキュリティを実現します。
ECDSAやECDHをはじめとする多くの応用例により、さまざまなセキュリティ分野で導入が進んでいます。
今後のデジタル社会において、効率的で安全な通信を実現するための重要な技術であるECCについて、その利点と注意点を理解し、適切に活用することが求められます。
